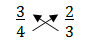The Illusion of Discovery
October 1, 2014
The Illusion of Discovery
Student-Centered on the Surface, Teacher-Centered Down Below
By Alfie Kohn
It’s not hard to recognize an utterly traditional classroom. If the teaching is heavily scripted and focused mostly on getting students to memorize right answers and practice skills by rote; if those students are sitting in rows, hunched over worksheets or being lectured at — well, geez, how can you not notice? It’s far trickier, however, to make sense of a class that has elements of collaboration and inquiry, and yet, on closer inspection, isn’t quite what it could be.
You have to look harder and think deeper to realize that what appears to be progressive instruction sometimes turns out to be more traditional and less impressive than it seemed at first glance. And if it’s your classroom, then acknowledging that possibility may require courage as well as insight. There are few barriers to change as intractable as the belief that one doesn’t need to change. When some teachers hear about a nontraditional curriculum or pedagogical approach, they instantly respond, “Oh, I’m already doing that.” And sometimes they are . . . sort of, but not entirely.
To acknowledge that one could be doing more — or, in some cases, less — can be difficult if you have a lot invested in believing that you have it all figured out. But there are also other reasons why it can be hard to acknowledge the need for change — reasons that explain why the status quo is so appealing in the first place. For one thing, traditional elements keep the teacher comfortably in control. If compliance is ultimately valued more than curiosity (even by some teachers who don’t recognize themselves in that description), then students may be given directions that are marvelously sophisticated, but the point is still to have them follow directions rather than play with unsanctioned or unconventional possibilities. For another thing, teachers may constrain the learning in subtle ways because of limitations in, and insecurity about, their understanding of the subject matter itself.
I wrote about this general phenomenon more than a decade ago in an article called “Almost There, But Not Quite” that dealt with general classroom dynamics. Now I’d like to focus on the way this plays out with academic lessons. Specifically, I’d like to share four passages from other authors who have explored the idea with remarkable acuity based on classroom observations. Three of these four offer illustrative vignettes that involve a single teacher. Although they were written years apart, each arrives at the same basic caution, which is why it’s fascinating to read them together.
*
1. Marlowe and Page
Jonah’s teacher, Mr. Stevens — young, energetic, charismatic — began his review of fractions and their relationships one Friday by passing out a variety of materials to each of the cooperative groups he had previously established: poster board, empty egg cartons, calculators, construction paper, markers, scissors. He asked simply, “Using the strategies we have talked about all week, please demonstrate that three-fourths is greater than two-thirds.” As Mr. Stevens circled the room, checking for understanding and periodically asking probing questions to individual groups about their work, the students attacked the problem with vigor, applying what they had been taught during the last four days. They divided the fractions (in order to compare the decimal amounts), filled the egg cartons, drew pie charts, and found common denominators. Mr. Stevens was thrilled that the students seemed to remember everything he had covered and as he made the rounds, he expressed his pride in them with great enthusiasm.
Jonah sat pensively, immobile.
While his group was pasting their work onto the poster board, he seemed to just stare at the numbers. And then, 15 minutes after the activity had begun, he said to Mr. Stevens, “I just noticed something…..that’s so cool. Look, Mr. Stevens, if you multiply from the bottom-up and across like this:
you get 9 on the left side and 8 on the right side. That’s really cool. Is that a way to show that three-fourths is greater than two-thirds? I mean will this always work? I think it will, but I’m not sure I really get it yet. Why does this work?…”
Uncertain of where Jonah was going, and nervous about his taking of such a divergent path, Mr. Stevens reminded Jonah that he was to use the strategies he had taught the class during the week. Mr. Stevens pointed out that there was no evidence that Jonah had done any work at all. Besides, Mr. Stevens had no idea if Jonah was on to something or not.
In the span of 15 minutes, Mr. Stevens communicated several potent lessons to Jonah, lessons that distinguish sham inquiry from a true constructivist classroom….Mr. Stevens believes, mistakenly, that his classroom provides opportunities for all students to engage in constructivist activities. But here is what Jonah learned:
1. It is more important that I answer my teacher’s questions than my own.
2. Independent thinking and problem solving is not to be pursued unless my teacher understands it and/or it conforms to teacher-approved methods and strategies.
3. It is very important that I move at the same pace and produce the same products as my peers.
4. My understanding can only be demonstrated by repeating back what has been transmitted and nothing more.
— Bruce A. Marlowe and Marilyn L. Page, Creating and Sustaining the Constructivist Classroom, 2nd ed. (Corwin Press, 2005): 120-21. Copyright © 2005 by Corwin Press
*
2. Cohen
[Having] found a new way to teach math…[involving] methods to engage students in actively understanding mathematics…Mrs. O was delighted with her students’ performance, and with her own accomplishments….But Mrs. O seemed to treat new mathematical topics as though they were part of traditional school mathematics. She used the new materials, but used them as though mathematics contained only right and wrong answers. She has revised the curriculum to help students understand math, but she conducts the class in ways that discourage exploration of students’ understanding….cobbl[ing] new ideas onto familiar practices….
For instance, Mrs. O regularly asked her second graders to work on ‘number sentences’…[to] make mathematics relationships more accessible by coming at them with ordinary language…[but] the class worked as though the lesson were a drill, reciting in response to the teachers’ queries. Students’ sentences were accepted if correct, and…turned down if incorrect and not written on the board….
[In using manipulatives,] Mrs. O seemed quite convinced that these physical experiences caused learning, that mathematical knowledge arose from the activities….[And when she asked students to] estimate how many large paper clips would be required to span one edge of the teacher’s desk…[there was no discussion of how one might go about making a reasonable guess. Moreover, estimation was presented] as a topic in its own right, rather than as a part of solving problems that came up in the course of studying mathematics….When the estimation example was finished, she turned the class to still another topic….
Mrs. O’s class was spatially and socially organized for…cooperative learning, but…the class was conducted in a highly structured and classically teacher-centered fashion….No student ever spoke to another about mathematical ideas as part of the public discourse….[Mrs. O] initiated nearly every interaction, whether with the entire class or one student. The students’ assigned role was to respond, not initiate….So even though most of the class usually was participating in the discourse, they participated on a narrow track, in which she maintained control of direction, content, and pace…..One reason that Mrs. O’s class was so smooth was that so many possible sources of roughness were choked off at the source….
Mrs. O did not see mathematics as a source of puzzles, as a terrain for argument, or as a subject in which questioning and explanation were essential to learning…[but] as a fixed body of truths…[which her job was to make] accessible to her students.
— David K. Cohen, “A Revolution in One Classroom: The Case of Mrs. Oublier,” Educational Evaluation and Policy Analysis 12 (1990): 311-29. Copyright © 1990 by the American Educational Research Association
*
3. Campbell
Here is a single summary paragraph from a research project in which primary-grade teachers in several urban schools were trained in constructivist math. Each of the six sentences in this very rich paragraph, which I’ve separated for emphasis, identifies an issue that could be the focal point of an extended cycle of classroom observation and conversation. — AK
[Some teachers who were invited to adopt a more thoughtful approach to teaching math have] moved considerably beyond routinized practice and direct instruction [but]…do not yet reflect on the understandings of their students, as these teachers are still focusing on their own behavior as they attempt to implement new instructional approaches.
They incorporate use of manipulative materials, but they frequently demonstrate how to use the materials, as if the use of the materials is the ultimate goal.
Although these teachers now permit the children to work in groups, they are unsure of how to monitor group learning, generally not questioning group activity as long as the group seems busy. These teachers may ask students to explain how they solved a problem, but they generally do not probe a student’s response, frequently moving on to another question if a correct answer is stated.
The teachers are trying to provide more wait time after their questions, often asking the children if anyone solved a problem in another way, but they are unsure of how to pursue incorrect responses or of how to relate responses [to one another].
In these classrooms, when a child asks a question, the teacher responds factually without probing the child’s reasoning or thinking.
— Patricia F. Campbell, “Empowering Children and Teachers in the Elementary Mathematics Classrooms of Urban Schools,” Urban Education 30 (1996): 466-67. Copyright © 1996 by Sage Publications, Inc.
*
4. Engel
A group of 21 boys and girls, all around ten years old, were sitting behind their desks. The teacher, Mrs. Parker, was explaining that the students were to form small groups and work on an activity to learn about how the ancient Egyptians had first invented wheels for transport in order to carry stones for their huge pyramids. She then organized the children into groups of three and invited each group to come up and get the materials they needed—a flat piece of wood with a metal eye at one end, some round wooden dowels, and a small measurement device that records Newtons, the amount of force required to pull an object at a given speed for a given distance. The device had a string with a hook attached to it so that children could hitch it to the bar. She also gave each group a worksheet to fill out, which included step-by-step instructions about what to do with the materials and a series of questions. Each group was to try pulling the wood piece along the floor, measuring how easily they could drag it both with and without dowels underneath it….
The children happily sorted into their assigned groups, materials in hand, and found a space on the floor to settle down and work….Then I noticed one group that seemed to have forgotten the worksheet and was instead intrigued by the equipment. The children were trying to figure out different ways to use the bar with the spring scale attached—yanking, pulling, and even at one point holding the string up high so that the bar was simply swinging in the air, hanging from the device. Then they stood the dowels up like columns and tried to balance the bar on the dowels. Finally, they tried surfing the bar along the surface of the dowels, which they had laid down to create something like a conveyer belt. At this point, Mrs. Parker…called out to the group, over the heads of her students, in a loud clear voice for all to hear, “OK, kids. Enough of that. I’ll give you time to experiment at recess. This is time for science.”
On the face of it, the teacher was doing just the kind of hands-on activity promoted by many educators….But just when the children in one group began to make the activity their own by following their own curiosity regarding the tools for the experiment—“What will happen if we pull it this way? What happens when we hang it that way?”—she stopped them. They had deviated from her plan. Ironically, this took place just as the children became interested in formulating and answering their own questions—when curiosity, the mechanism that underlies the best learning, kicked in.
— Susan Engel, “Children’s Need to Know: Curiosity in Schools,” Harvard Educational Review 81 (2011): 625-26. Copyright © 2011 by the President and Fellows of Harvard College
*
While all of these examples involve elementary school math and science, I’d invite you to consider whether they can’t be applied to older students and other subjects as well. Implicitly, the authors are providing us with a lesson in how to observe a lesson critically: what to look for in a classroom and how to look hard to find it. These passages may be useful for teacher-educators and their students, school administrators, and others involved in professional development. But their real power emerges when teachers themselves are invited to reflect on their craft and to ask “Am I doing all I can to nourish students’ curiosity, to help them think for themselves and with one another?”